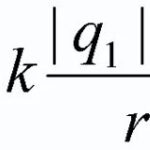Lorentzova sila i vlada lijeva ruka. Kretanje nabijenih čestica u magnetskom polju

Postavljen u magnetsko polje dirigentkroz koji je prošao struja, na njega djeluje sila Ampera $FA$ , a njegova se vrijednost može izračunati pomoću sljedeće formule:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

gdje $ja$ i $l$ - jačina struje i duljina vodiča, $B$ – indukcija magnetskog polja, $\alfa$ - kut između smjerova jačine struje i magnetske indukcije. Zašto se ovo događa?

Lorentzova sila. Gibanje nabijene čestice u magnetskom polju.

Sadržaj

1 Što je Lorentzova sila - određivanje kada se pojavi, dobivanje formule
2 Određivanje smjera Lorentzove sile pomoću pravila lijeve ruke
3 Gibanje nabijene čestice u magnetskom polju
4 Primjena Lorentzove sile u inženjerstvu

Što je Lorentzova sila - određivanje kada se pojavi, dobivanje formule

Poznato je da je električna struja uređeno kretanje nabijenih čestica. Također je utvrđeno da je tijekom kretanja u magnetskom polju svaka od ovih čestica podvrgnuta djelovanju sile. Da bi se pojavila sila, čestica mora biti u pokretu.

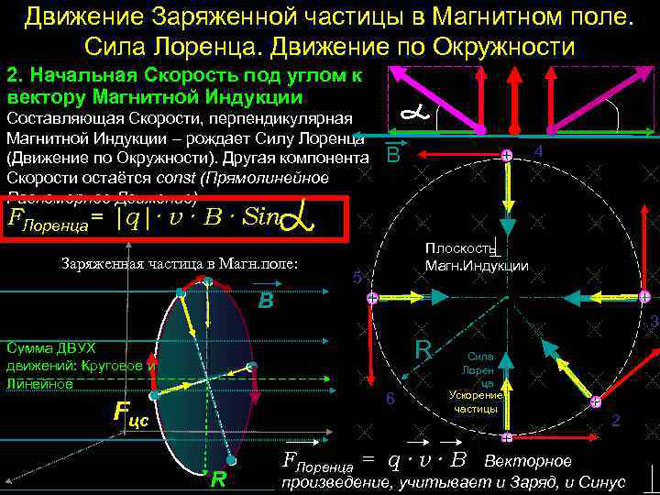
Lorentzova sila je sila koja djeluje na električki nabijenu česticu dok se kreće u magnetskom polju.Njegov je smjer ortogonan na ravninu u kojoj leže vektori brzine čestica i jakosti magnetskog polja. Rezultanta Lorentzovih sila je Amperova sila. Znajući to, možemo izvesti formulu za Lorentzovu silu.

Vrijeme potrebno da čestica prođe kroz segment vodiča, $t = \frac {l}{v}$ , gdje $l$ - duljina segmenta, $v$ je brzina čestice. Ukupni naboj prenesen za to vrijeme kroz poprečni presjek vodiča, $Q = I\cdot t$ . Zamjenjujući ovdje vrijednost vremena iz prethodne jednadžbe, imamo

$Q = \frac {I\cdot l}{v}$ (2)

U isto vrijeme $F_A=F_L\cdot N$ , gdje $N$ je broj čestica u razmatranom vodiču. Pri čemu $N = \frac {Q}{q}$ , gdje $q$ je naboj jedne čestice. Zamjena vrijednosti u formulu $P$ iz (2) može se dobiti:

$N = \frac {I\cdot l}{v\cdot q}$

Na ovaj način,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Koristeći (1), prethodni izraz se može zapisati kao

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Nakon kontrakcija i transfera pojavljuje se formula za izračun Lorentzove sile

$F_L = q\cdot v\cdot B\cdot sin\alpha$

S obzirom da je formula zapisana za modul sile, ona se mora napisati na sljedeći način:

Pročitajte također: Kako pretvoriti ampere u vate i obrnuto?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Jer $sin\alpha = sin(180^{\circ} - \alpha)$ , tada za izračunavanje modula Lorentzove sile nije važno kamo je brzina usmjerena, - u smjeru jakosti struje ili protiv, - i možemo reći da $\alfa$ je kut koji čine vektori brzine čestice i magnetske indukcije.

Pisanje formule u vektorskom obliku izgledat će ovako:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\puta \vec{B}]$ je križni proizvod, čiji je rezultat vektor s modulom jednakim $v\cdot B\cdot sin\alpha$ .

Na temelju formule (3) možemo zaključiti da je Lorentzova sila maksimalna u slučaju okomitih smjerova električne struje i magnetskog polja, tj. $\alpha = 90^{\circ}$ , i nestaju kada su paralelni ( $\alpha = 0^{\circ}$ ).

Treba imati na umu da za dobivanje točnog kvantitativnog odgovora - na primjer, pri rješavanju zadataka - treba koristiti jedinice SI sustava u kojem se magnetska indukcija mjeri u teslasima (1 T = 1 kg s⁻²·ALI⁻¹), sila - u Newtonima (1 N = 1 kg m/s²), jačina struje - u amperima, naboj u kulonima (1 C = 1 A s), duljina - u metrima, brzina - u m / s.

Određivanje smjera Lorentzove sile pomoću pravila lijeve ruke

Budući da se Lorentzova sila manifestira kao Amperova sila u svijetu makroobjekata, za određivanje njezina smjera može se koristiti pravilo lijeve ruke.

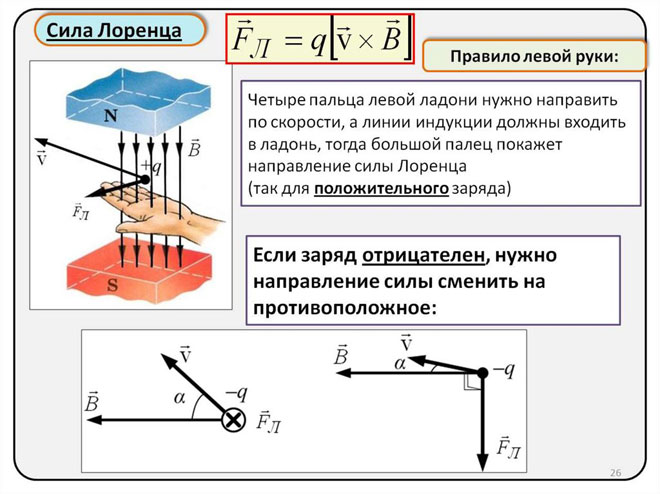
Određivanje smjera djelovanja Lorentzove sile prema pravilu lijeve ruke.

Lijevu ruku trebate staviti tako da otvoreni dlan bude okomit na i prema linijama magnetskog polja, četiri prsta treba ispružiti u smjeru jačine struje, tada će Lorentzova sila biti usmjerena tamo gdje pokazuje palac, što treba biti savijen.

Gibanje nabijene čestice u magnetskom polju

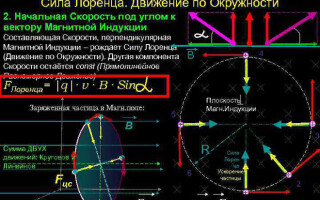
U najjednostavnijem slučaju, to jest, kada su vektori magnetske indukcije i brzine čestice ortogonalni, Lorentzova sila, koja je okomita na vektor brzine, može promijeniti samo svoj smjer. Veličina brzine, dakle, i energije ostat će nepromijenjeni. To znači da Lorentzova sila djeluje po analogiji sa centripetalnom silom u mehanici, a čestica se giba u krug.

Pročitajte također: Koliko je wata u kilovatu?

U skladu s Newtonovim II zakonom ( $F = m\cdot a$ ) možemo odrediti polumjer rotacije čestice:

$N = \frac {m\cdot v}{q\cdot B}$ .

Treba napomenuti da s promjenom specifičnog naboja čestice ( $\frac {q}{m}$ ) mijenja se i polumjer.

U ovom slučaju, period rotacije T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Ne ovisi o brzini, što znači da će međusobni položaj čestica s različitim brzinama biti nepromijenjen.

Gibanje nabijene čestice u jednoličnom magnetskom polju.

U složenijem slučaju, kada je kut između brzine čestice i jakosti magnetskog polja proizvoljan, kretat će se po zavojnoj putanji - translacijsko zbog komponente brzine usmjerene paralelno s poljem, a duž kružnice pod utjecajem njezine okomita komponenta.

Primjena Lorentzove sile u inženjerstvu

Kineskop

Kineskop, koji je donedavno, kada ga je zamijenio LCD (ravni) ekran, u svakom televizoru nije mogao raditi bez Lorentzove sile. Za formiranje televizijskog rastera na ekranu iz uskog toka elektrona koriste se zavojnice za skretanje, u kojima se stvara linearno promjenjivo magnetsko polje. Horizontalne zavojnice pomiču snop elektrona s lijeva na desno i vraćaju ga natrag, kadrovske zavojnice su odgovorne za okomito kretanje, pomičući snop koji ide vodoravno od vrha do dna. Isti princip se koristi u osciloskopi - uređaji koji se koriste za proučavanje izmjeničnog električnog napona.

masspektrograf

Maseni spektrograf je uređaj koji koristi ovisnost polumjera rotacije nabijene čestice o njenom specifičnom naboju. Princip njegovog rada je sljedeći:

Izvor nabijenih čestica, koje dobivaju brzinu uz pomoć umjetno stvorenog električnog polja, stavlja se u vakuumsku komoru kako bi se isključio utjecaj molekula zraka. Čestice izlete iz izvora i, prošavši duž luka kruga, udare u fotografsku ploču, ostavljajući na njoj tragove. Ovisno o specifičnom naboju mijenja se polumjer putanje, a time i točka udara. Ovaj polumjer je lako izmjeriti, a znajući ga, možete izračunati masu čestice. Uz pomoć masenog spektrografa, primjerice, proučavan je sastav mjesečevog tla.

Pročitajte također: Koja su zanimanja vezana uz električnu energiju

Ciklotron

Neovisnost perioda, a time i frekvencije rotacije nabijene čestice od njezine brzine u prisutnosti magnetskog polja, koristi se u uređaju koji se zove ciklotron i dizajniran za ubrzavanje čestica do velikih brzina. Ciklotron su dva šuplja metalna polucilindra - dee (po obliku, svaki od njih podsjeća na latinsko slovo D) postavljene ravnim stranicama jedna prema drugoj na maloj udaljenosti.

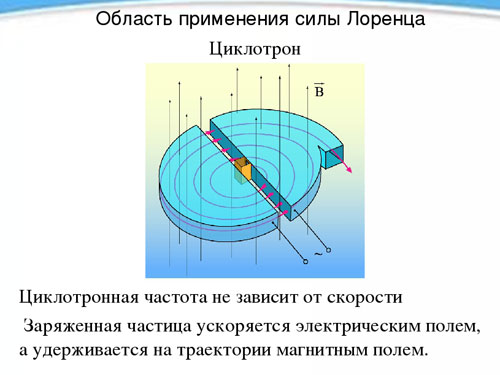
Ciklotron - primjena Lorentzove sile.

Dijelovi su smješteni u stalno jednolično magnetsko polje, a između njih se stvara izmjenično električno polje čija je frekvencija jednaka frekvenciji rotacije čestice, određenoj jakosti magnetskog polja i specifičnim nabojem. Dobivajući dva puta tijekom razdoblja rotacije (tijekom prijelaza s jedne točke na drugu) pod utjecajem električnog polja, čestica se svaki put ubrzava, povećavajući polumjer putanje i u određenom trenutku, nakon što je dobila željenu brzinu, izleti iz uređaja kroz rupu. Na taj se način proton može ubrzati do energije od 20 MeV (megaelektronvolt).

Magnetron

Uređaj koji se zove magnetron, koji je ugrađen u svaki mikrovalna pećnica, je još jedan predstavnik uređaja koji koriste Lorentzovu silu. Magnetron se koristi za stvaranje snažnog mikrovalnog polja, koje zagrijava unutarnji volumen pećnice u koju se stavlja hrana. Magneti uključeni u njegov sastav ispravljaju putanju kretanja elektrona unutar uređaja.

Zemljino magnetsko polje

A u prirodi Lorentzova sila igra iznimno važnu ulogu za čovječanstvo. Njegova prisutnost omogućuje Zemljinom magnetskom polju da zaštiti ljude od smrtonosnog ionizirajućeg zračenja svemira. Polje ne dopušta nabijenim česticama da bombardiraju površinu planeta, prisiljavajući ih na promjenu smjera.

Slični članci: